Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2025
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
1.
Con los vectores $\overrightarrow{\boldsymbol{A}}$ y $\overrightarrow{\boldsymbol{B}}$ de la Figura 1, use un dibujo a escala para obtener la magnitud y la dirección de:
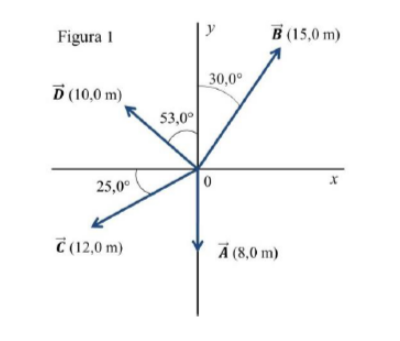
b) Con base en sus respuestas, determine la magnitud y la dirección de: $-\overrightarrow{\boldsymbol{A}}-\overrightarrow{\boldsymbol{B}}$ y $\overrightarrow{\boldsymbol{B}}-\overrightarrow{\boldsymbol{A}}$.
b) Con base en sus respuestas, determine la magnitud y la dirección de: $-\overrightarrow{\boldsymbol{A}}-\overrightarrow{\boldsymbol{B}}$ y $\overrightarrow{\boldsymbol{B}}-\overrightarrow{\boldsymbol{A}}$.
Respuesta
Parece que otra vez nos vamos a tener que poner a hacer más cuentas y gráficos, y esto viene para largo... pero no, si lo pensamos tranqui unos minutos esto va a salir en dos patadas:
Reportar problema
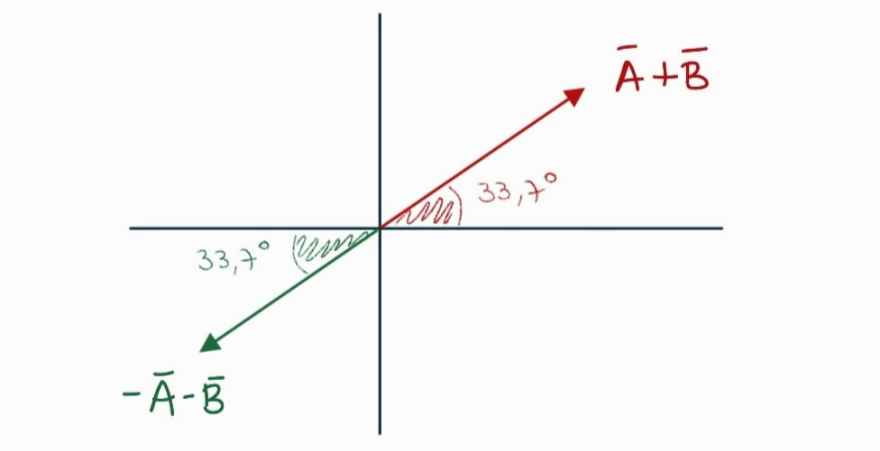
➡️ Hace un ratito nosotros encontramos el módulo y la dirección de $\vec{A} + \vec{B}$. Ahora, fijate que si hacemos...
$-1 \cdot (\vec{A} + \vec{B}) = -\vec{A} - \vec{B}$
Es decir, ¡sólo estamos multiplicando al vector $\vec{A} + \vec{B}$ por $-1$!
Usando lo que vimos en las clases de vectores, multiplicar por un escalar negativo nos cambia el sentido y, como justo es $-1$ (o sea, un escalar con módulo exactamente $1$), no nos modifica el módulo del vector.
Por lo tanto, su módulo también es $9.01$ y forma un ángulo de $33.7°$ con el semieje negativo de las $x$. Fijate que así ambos vectores tienen la misma dirección (estan "apoyados" sobre la misma recta), sólo tienen sentidos opuestos.
Aclaración: En las respuestas de la guía reportan el ángulo que forma con el semieje positivo de las x, por eso la respuesta "parece distinta", pero estamos hablando de la misma dirección.
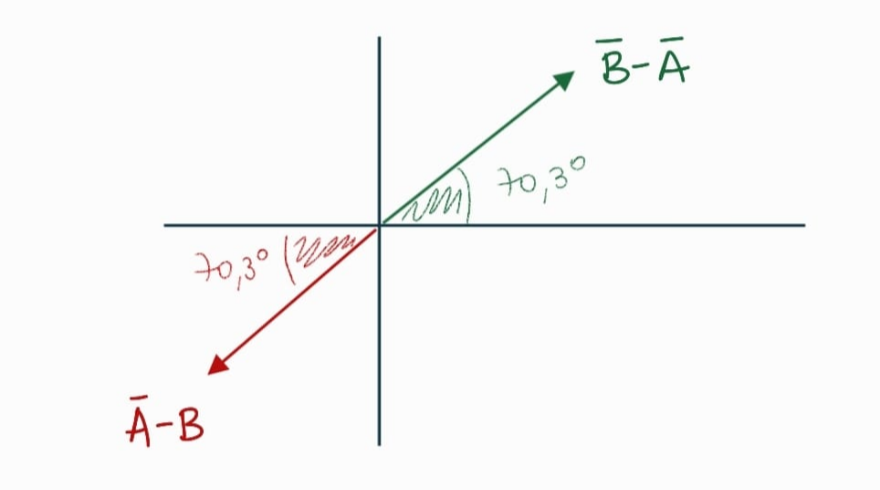
➡️ Te imaginas ahora que algo parecido va a ocurrir con el otro vector, no? Nosotros ya teníamos todo calculado para el vector $\vec{A} - \vec{B}$. Fijate ahora que el vector que nos piden en este ítem, $\vec{B} - \vec{A}$, no es otra cosa que...
$-1 \cdot (\vec{A} - \vec{B}) = \vec{B} - \vec{A}$
Así que solamente tenemos que multiplicar por el escalar $-1$ al vector que ya conocíamos. Eso mantiene el mismo módulo y dirección, pero invierte el sentido. Nos queda así:
Por lo tanto, su módulo también es $22.3$ y forma un ángulo de $70.3°$ con el semieje positivo de las $x$. Fijate que así ambos vectores tienen la misma dirección (estan "apoyados" sobre la misma recta), sólo tienen sentidos opuestos.
Iniciá sesión o
Registrate para
dejar
tu
comentario.
🤖 ExaBoti
Esta conversación es privada
🤖 ExaBoti (privado)